Segmentación de clientes de tarjetas de crédito - Aprendizaje supervisado y no supervisado
Las tarjetas de crédito han dejado de ser un símbolo de estatus para convertirse en una herramienta financiera accesible y versátil. Su uso varía según el perfil del cliente, desde quienes las ven como un medio de financiamiento hasta quienes buscan maximizar beneficios.

Las tarjetas de crédito han dejado de ser un símbolo de estatus para convertirse en una herramienta financiera accesible y versátil. Su uso varía según el perfil del cliente, desde quienes las ven como un medio de financiamiento hasta quienes buscan maximizar beneficios. Para comprender estos patrones, analizamos a 9,000 titulares activos mediante 17 variables clave, aplicando técnicas de segmentación. Esto nos permitió identificar grupos de usuarios con comportamientos similares, simplificando el análisis sin perder información valiosa.
Para llevar a cabo el análisis, consideramos una serie de variables clave que nos permiten entender los hábitos de uso de las tarjetas de crédito. A continuación, presentamos las principales variables y su correspondencia en la base de datos.
| Categoría | Variable | Nombre en la Base de Datos |
|---|---|---|
| Datos Financieros | Saldo | BALANCE |
| Frecuencia Saldo | BALANCE_FREQUENCY | |
| Transacciones | Compras Totales | PURCHASES |
| Compras Únicas | ONEOFF_PURCHASES | |
| Compras a Plazos | INSTALLMENTS_PURCHASES | |
| Otros Datos | Efectivo Adelantado | CASH_ADVANCE |
Aprendizaje No Supervisado: Descubriendo Patrones sin Etiquetas
El análisis no supervisado se basa en el procesamiento de datos sin etiquetas predefinidas, lo que permite identificar estructuras ocultas en la información. Las metodologías multivariantes son fundamentales para extraer conocimientos relevantes y reducir la complejidad dimensional.
Una de las técnicas más utilizadas es el Análisis de Componentes Principales (PCA), desarrollado por Karl Pearson en 1901. Este método permite simplificar el conjunto de datos transformando variables originales en nuevas variables denominadas componentes principales, definidas por la siguiente combinación lineal:
Para clasificar los datos, se emplea el método de Ward, introducido por Joe H. Ward. Este algoritmo agrupa los individuos minimizando la suma de las distancias cuadráticas dentro de cada clúster, logrando así una segmentación óptima basada en similitudes.
Vamos a R
Señalamos que el código y los resultados están en español. Esto fue realizado por Kleiner J. Balanta
Código
Ver Código
library(tidyverse)
library(dendextend)
library(factoextra)
library(FactoClass)
library(corrplot)
library(caret)
library(stats)
library(dplyr)
Datos_Base<-read.csv("https://github.com/juniorjb5/Data/blob/main/TarjetasCredito.csv"
,header = TRUE, sep = "," ,dec = ".", row.names = 1) #En ese link consigues los datos
is.na(Datos_Base) # True: Nas y False: Datos
sum(is.na(Datos_Base)) #314 Na's
sum(complete.cases(is.na(Datos_Base))) #8950 Datos
# De 9264 observaciones, solo 8950 tienen observaciones sin Na's. Es decir, trabajamos
#con el 96,51% de las observaciones de la base de datos original. Aun es una buena base de datos.
Datos<-na.omit(Datos_Base)
View(Datos)
#Cambio de nombre de las columnas de la base de datos
Datos <- Datos %>%
rename(Saldo=BALANCE,Frec_Saldo=BALANCE_FREQUENCY,
Compras=PURCHASES,Compras_UnaVez=ONEOFF_PURCHASES,
Compras_aPlazos=INSTALLMENTS_PURCHASES,Efectivo_Adelantado=CASH_ADVANCE,
Frec_Compras=PURCHASES_FREQUENCY,Fre_Compras_UnaVez=ONEOFF_PURCHASES_FREQUENCY,
frec_Compras_aPlazos=PURCHASES_INSTALLMENTS_FREQUENCY,Frec_Efectivo_Adelantado=CASH_ADVANCE_FREQUENCY,
Num_trans_Efectivo_Adelantado=CASH_ADVANCE_TRX ,Num_trans_Compras=PURCHASES_TRX,
Limite_Credito=CREDIT_LIMIT ,Pagos_Realizados=PAYMENTS,Num_Min_Pagos_Realizados=MINIMUM_PAYMENTS
,Porcent_PagosCompletos_Realizados=PRC_FULL_PAYMENT
,Tenencia_Servicio=TENURE)
matriz_correlacion<- cor(Datos)
print(matriz_correlacion)
Alta_Correlacion <- findCorrelation(matriz_correlacion,cutoff = 0,1)
print(names(Datos[,Alta_Correlacion]))
x11()
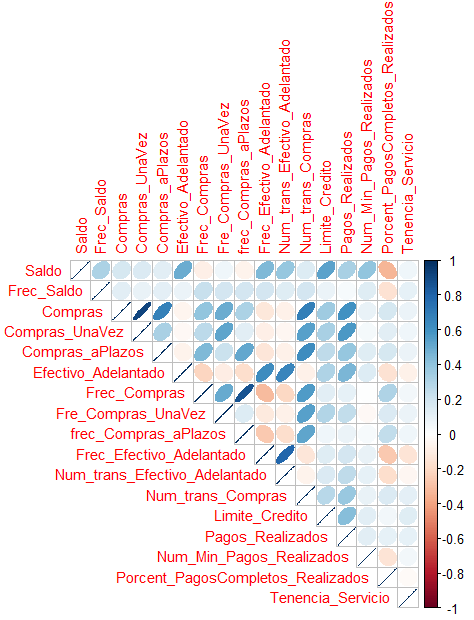
corrplot(cor(Datos), type="upper", method="ellipse", tl.cex=0.9)
La figura muestra la correlación entre todas las variables de la base de datos
Ver Código
# Componentes: Varianza explicada
res.pca <- prcomp(Datos, scale = TRUE)
res.pca[[1]]
fviz_eig(res.pca,ylab = "porcentaje de varianza explicada",
xlab= "numero de componentes", main = "." ,barfill = "#0B7D75",addlabels = TRUE) + theme_classic()
Existen diferentes variedades de criterios que ayudan a seleccionar el número de componentes, en este caso se decidió utilizar uno de los más famosos llamado criterio de Kaiser. Para ello se hallaron los valores propios de los 5 primeros componentes, que se reflejan en la siguiente tabla
| PC 1 | PC 2 | PC 3 | PC 4 | PC 5 |
|---|---|---|---|---|
| 2.1516 | 1.8611 | 1.2313 | 1.1347 | 1.0330 |
El criterio de Kaiser recomienda seleccionar 5 componentes. Sin embargo, el valor de los valores propios entre los componentes 3, 4 y 5 no varía mucho en comparación con los 2 primeros componentes. Ante esta observación, se decidió trazar un diagrama de barras con el porcentaje de varianza o explicación aportado por cada componente, con el fin de tener una visión más amplia y detallada de la elección de los componentes
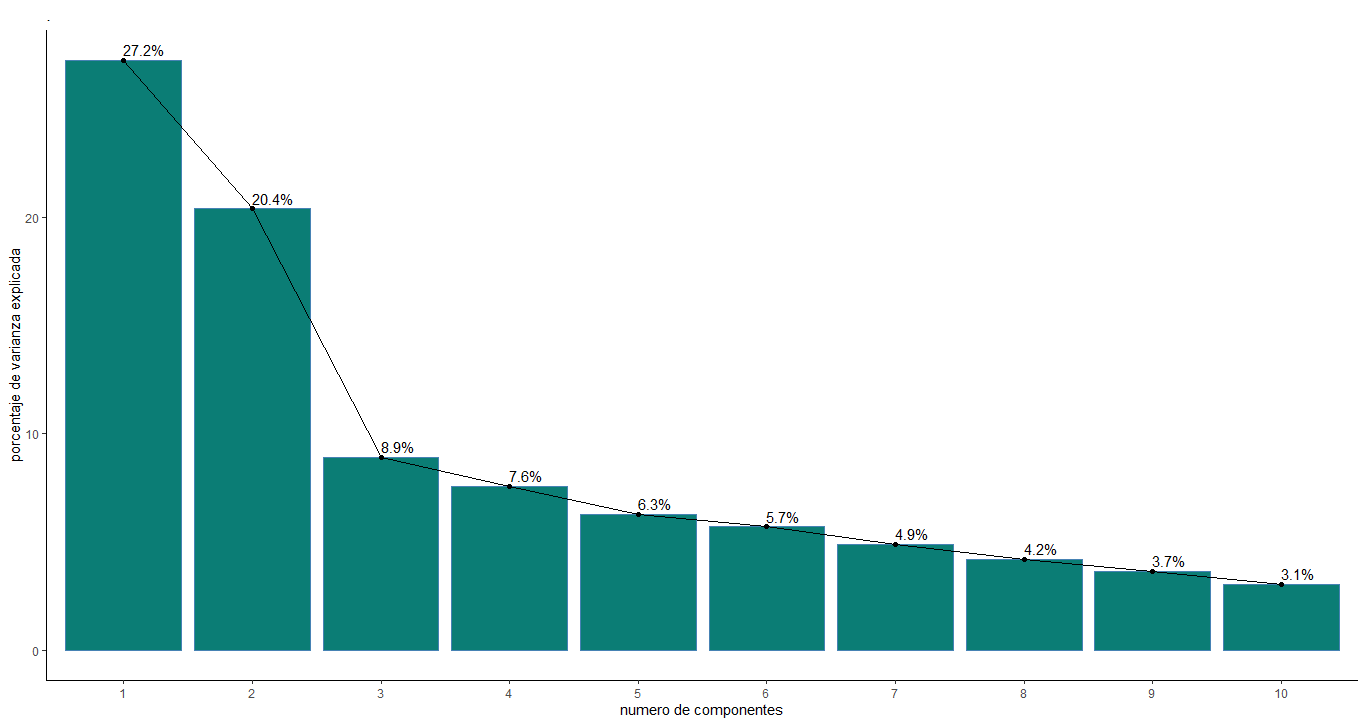
El gráfico muestra un comportamiento interesante, los componentes 3, 4 y 5 sí cumplen con el criterio de Kaiser como se mencionó anteriormente, pero entre estos el porcentaje de información explicada no tiene mucha diferencia, por lo que se puede decir que hay ruido entre ellos. . Por esta razón, se decidió utilizar 3 componentes, es decir, tenemos un porcentaje de varianza de aproximadamente 56.5% para nuestro análisis.
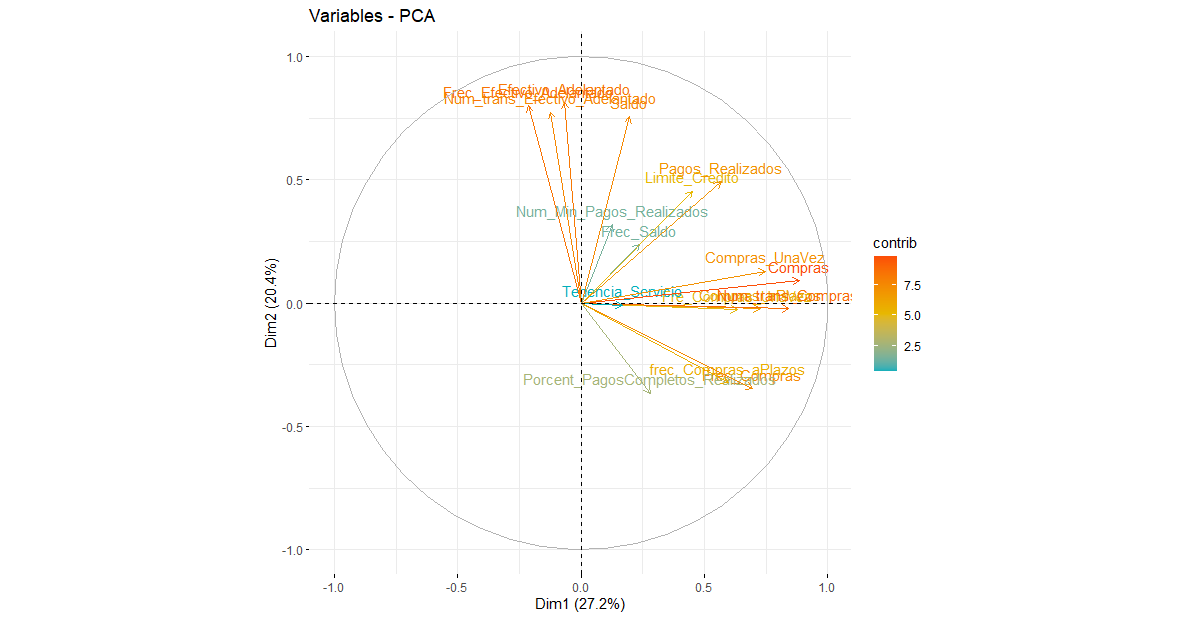
Con base a las variables que más influyen en la explicación del primer componente, se denominó a este factor poder adquisitivo; ya que su definición agrupa y relaciona las variables. «El poder adquisitivo, poder de compra o poder adquisitivo es la cantidad de bienes o servicios que se pueden obtener con una cantidad fija de dinero en función del nivel de precios»
En cuanto al segundo componente, se denominó capacidad de pago, ya que de acuerdo con el Banco de México (Banxico), hay usuarios que tienen ingresos fijos mensuales y al realizar sus compras hacen sus pagos en efectivo o a fin de mes para evitar intereses y construir un buen historial crediticio, además de mantener el acceso a las recompensas y beneficios que se ofrecen.
Finalmente, el tercer componente se denominó consumo excesivo, de acuerdo con Marco Carrera, director de Estudios de Mercado de la Comisión Nacional para la Defensa de los Usuarios de Servicios Financieros (Condusef) en 2009, las personas que frecuentemente adquieren desde compras que satisfacen sus necesidades básicas son consideradas personas que caen en la tendencia del consumismo, por lo que ven la necesidad de pagar el costo mínimo de las tarjetas de crédito y así mantener su límite de crédito y todos los beneficios que esto conlleva.
Ver Código
fviz_pca_ind(res.pca,
col.ind = "cos2", # Color by the quality of representation
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = FALSE # Avoid text overlapping
)
fviz_pca_var(res.pca,
col.var = "contrib", # Color by contributions to the PC
gradient.cols = c("#00AFBB", "#E7B800", "#FC4E07"),
repel = FALSE # Avoid text overlapping
)
fviz_pca_biplot(res.pca, repel = FALSE,
col.var = "#2E9FDF", # Variables color
col.ind = "#696969" # Individuals color
)
eig.val <- get_eigenvalue(res.pca)
eig.val #Valores propios de los componentes compuestos
res.var <- get_pca_var(res.pca)
res.var$coord # Coordinates
res.var$contrib # Contribuccion de las variables a los ejes
res.var$cos2 # Quality of representation
View(res.var$contrib[,1:3]) # Miro los 3 primeros factores
# Resultados por individuos
res.ind <- get_pca_ind(res.pca)
res.ind$coord # Coordinates
res.ind$contrib # Contribuccion a los componentes
res.ind$cos2 # Quality of representation
View(res.ind$contrib[,1:3]) # Miro los tres primeros factores
Ver Código
resultado_ACP<-FactoClass(Datos,dudi.pca)
3
3
4
resultado_ACP$cluster
NuevaBase<-data.frame(Cluster=resultado_ACP$cluster,Datos) # unir la nueva base de datos con la nueva variable cluster
View(NuevaBase)
plot(resultado_ACP$dudi) # Grafico del an?lisis
s.corcircle((resultado_ACP$dudi)$co)
s.label((resultado_ACP$dudi)$li,label=row.names(Datos)) #Graf. Individuos
s.label((resultado_ACP$dudi)$co,xax=1,yax=2,sub="Componente 1 y 2",possub="bottomright",) #Graf. Variables
s.label((resultado_ACP$dudi)$co,xax=1,yax=3,sub="Componente 1 y 3",possub="bottomright",) #Graf. Variables
s.label((resultado_ACP$dudi)$co,xax=2,yax=1,sub="Componente 2 y 1",possub="bottomright",) #Graf. Variables
s.label((resultado_ACP$dudi)$co,xax=2,yax=3,sub="Componente 2 y 3",possub="bottomright",) #Graf. Variables
s.label((resultado_ACP$dudi)$co,xax=3,yax=1,sub="Componente 3 y 1",possub="bottomright",) #Graf. Variables
s.label((resultado_ACP$dudi)$co,xax=3,yax=2,sub="Componente 3 y 2",possub="bottomright",) #Graf. Variables
x11()
scatter(resultado_ACP$dudi,xax=1,yax=2,sub="Componente 1 y 2",possub="bottomright") # Graf. Conjuntos
X11()
scatter(resultado_ACP$dudi,xax=1,yax=3,sub="Componente 1 y 3",possub="bottomright")
X11()
scatter(resultado_ACP$dudi,xax=2,yax=1,sub="Componente 2 y 1",possub="bottomright")
X11()
scatter(resultado_ACP$dudi,xax=2,yax=3,sub="Componente 2 y 3",possub="bottomright")
X11()
scatter(resultado_ACP$dudi,xax=3,yax=1,sub="Componente 3 y 1",possub="bottomright")
X11()
scatter(resultado_ACP$dudi,xax=3,yax=2,sub="Componente 3 y 2",possub="bottomright")
Grupo<-NuevaBase$Cluster
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 1 y 2",possub="bottomright",xax=1,yax=2,col=c(1,2,3,4))
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 1 y 3",possub="bottomright",xax=1,yax=3,col=c(1,2,3,4))
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 2 y 1",possub="bottomright",xax=2,yax=1,col=c(1,2,3,4))
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 2 y 3",possub="bottomright",xax=2,yax=3,col=c(1,2,3,4))
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 3 y 1",possub="bottomright",xax=3,yax=1,col=c(1,2,3,4))
X11()
s.class((resultado_ACP$dudi)$li,Grupo,sub="Componentes 3 y 2",possub="bottomright",xax=1,yax=2,col=c(1,2,3,4))
#importante
#DescripciÓn de los grupos (Análisis de medias)
resultado_ACP$carac.cont
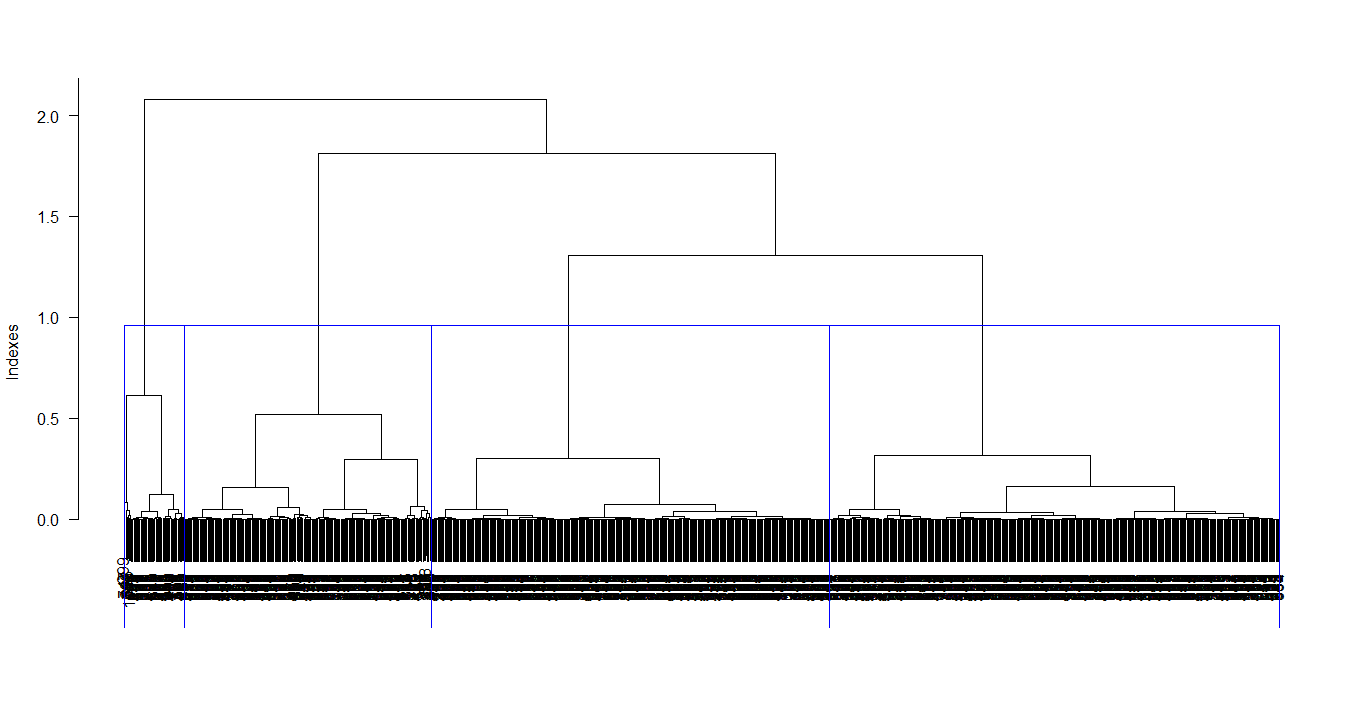
Dendogram
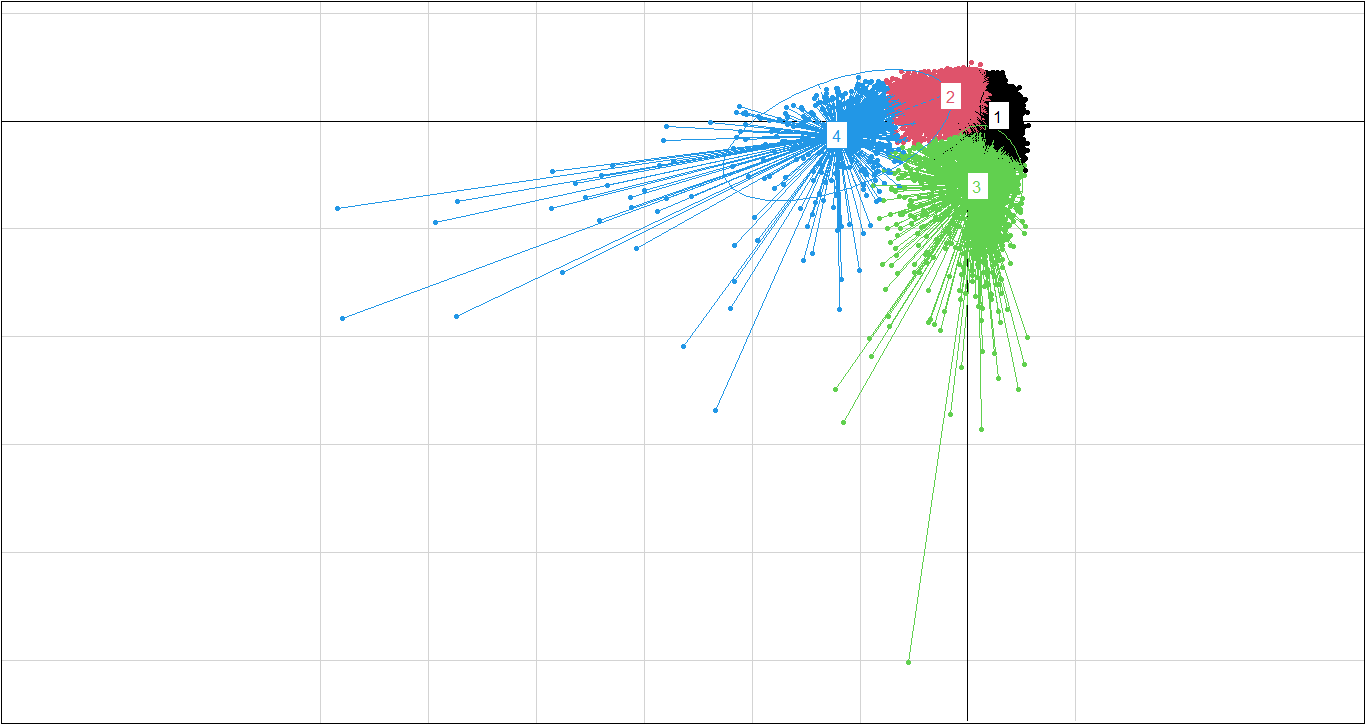
PC1 vs PC2
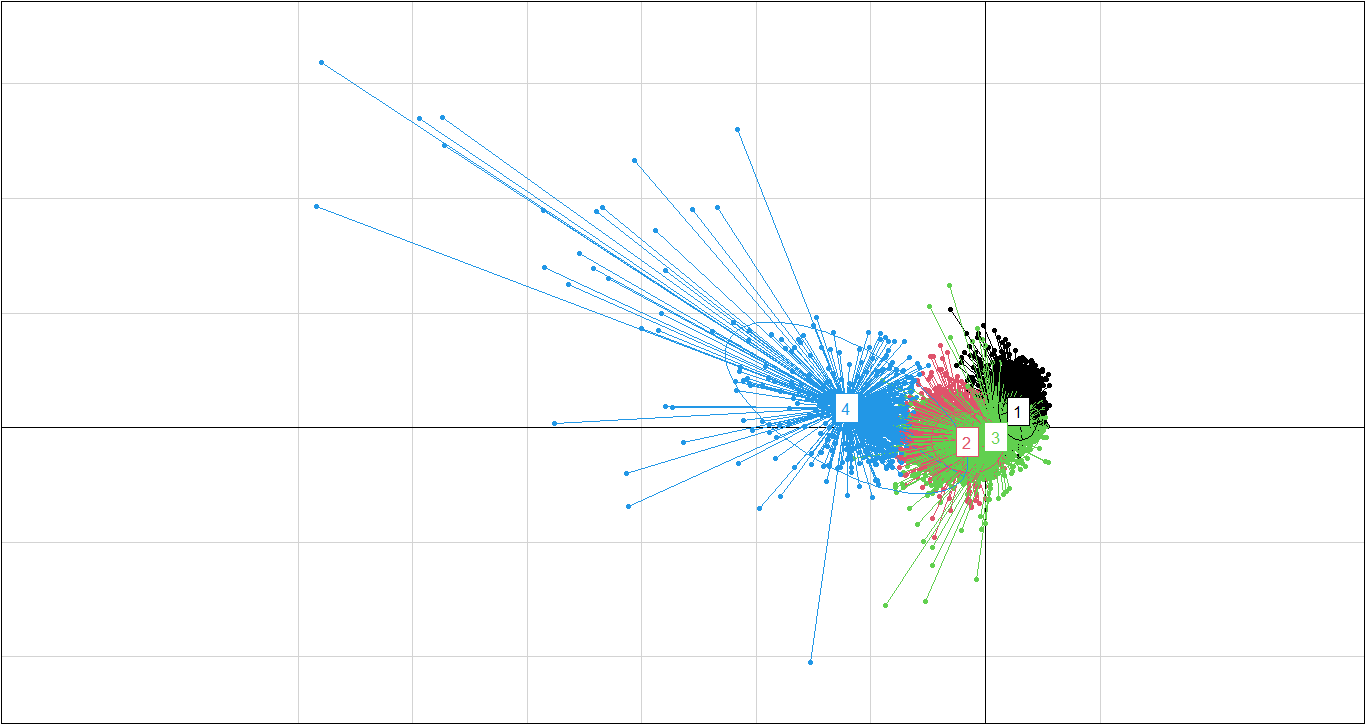
PC1 vs PC3
Caracterización de las clases
Ver Código
class: 1
Test.Value Class.Mean Frequency Global.Mean
Frec_Compras 68.218 0.938 2657 0.496
frec_Compras_aPlazos 61.895 0.767 2657 0.369
Fre_Compras_UnaVez 40.837 0.404 2657 0.206
Compras_aPlazos 34.321 929.010 2657 420.844
Compras 28.956 2038.379 2657 1025.434
Porcent_PagosCompletos_Realizados 25.250 0.280 2657 0.159
Frec_Saldo 24.426 0.977 2657 0.895
Compras_UnaVez 18.570 1109.784 2657 604.901
Limite_Credito 13.143 5298.450 2657 4522.091
Pagos_Realizados 5.278 2032.412 2657 1784.478
Saldo -7.423 1350.131 2657 1601.225
Efectivo_Adelantado -21.528 256.949 2657 994.176
Frec_Efectivo_Adelantado -28.902 0.043 2657 0.138
------------------------------------------------------------
class: 2
Test.Value Class.Mean Frequency Global.Mean
Frec_Efectivo_Adelantado -10.482 0.118 4960 0.138
Num_Min_Pagos_Realizados -14.953 535.657 4960 864.305
Porcent_PagosCompletos_Realizados -16.299 0.115 4960 0.159
Efectivo_Adelantado -18.377 633.015 4960 994.176
Compras_UnaVez -25.412 208.401 4960 604.901
Pagos_Realizados -28.894 1005.618 4960 1784.478
Saldo -29.143 1035.473 4960 1601.225
Frec_Saldo -31.424 0.835 4960 0.895
Compras -35.002 322.735 4960 1025.434
Compras_aPlazos -36.037 114.633 4960 420.844
Limite_Credito -36.397 3288.275 4960 4522.091
Fre_Compras_UnaVez -37.545 0.102 4960 0.206
frec_Compras_aPlazos -50.555 0.182 4960 0.369
Frec_Compras -55.501 0.290 4960 0.496
------------------------------------------------------------
class: 3
Test.Value Class.Mean Frequency Global.Mean
Efectivo_Adelantado 60.918 4968.608 942 994.176
Frec_Efectivo_Adelantado 60.158 0.511 942 0.138
Saldo 53.513 5049.907 942 1601.225
Limite_Credito 32.142 8139.124 942 4522.091
Pagos_Realizados 24.556 3981.927 942 1784.478
Num_Min_Pagos_Realizados 22.039 2472.399 942 864.305
Frec_Saldo 12.669 0.976 942 0.895
Compras_UnaVez -4.497 371.965 942 604.901
Fre_Compras_UnaVez -6.205 0.149 942 0.206
Compras -6.405 598.583 942 1025.434
Compras_aPlazos -6.882 226.726 942 420.844
Porcent_PagosCompletos_Realizados -13.818 0.033 942 0.159
frec_Compras_aPlazos -14.172 0.195 942 0.369
Frec_Compras -15.868 0.300 942 0.496
------------------------------------------------------------
class: 4
Test.Value Class.Mean Frequency Global.Mean
Compras 63.180 16559.006 77 1025.434
Compras_UnaVez 57.402 11573.696 77 604.901
Pagos_Realizados 44.627 16516.810 77 1784.478
Compras_aPlazos 43.863 4985.310 77 420.844
Limite_Credito 20.325 12959.740 77 4522.091
Fre_Compras_UnaVez 17.557 0.804 77 0.206
Saldo 12.270 4518.465 77 1601.225
Frec_Compras 9.616 0.934 77 0.496
frec_Compras_aPlazos 9.027 0.777 77 0.369
Porcent_PagosCompletos_Realizados 7.584 0.414 77 0.159
Num_Min_Pagos_Realizados 5.865 2442.863 77 864.305
Frec_Saldo 3.347 0.974 77 0.895
Frec_Efectivo_Adelantado -2.465 0.081 77 0.138
La primera clase está formada por los clientes con el saldo de tarjeta de crédito más alto, se puede deducir que tienen un buen sueldo o ganan mucho dinero. Estas personas prefieren no pagar sus compras con tarjeta de crédito, prefieren retirar efectivo por adelantado para realizar dichas compras. Su límite de crédito es muy alto, ya que sus ingresos son elevados y el tiempo con el que pagan sus adelantos en efectivo es muy bajo. En definitiva, son personas ricas que no compran con su tarjeta, quizás para que no quede constancia de sus compras. En cuanto al nivel social, son personas de renta alta que prefieren evitar el registro de sus transacciones bancarias. Esta clase de clientes se clasificó como clientes pasivos.
| Clase | Característica | Nivel |
|---|---|---|
| Clientes Pasivos | Poder adquisitivo | Bajo |
| Capacidad de pago | Alto | |
| Consumo excesivo | Bajo |
La segunda clase está formada por clientes con saldos muy bajos, en realidad la segunda más baja entre las clases. Son la clase con el menor índice de compras, ya sea en compras instantáneas o a plazos. Lo anterior se refleja en su límite de crédito, ya que al ganar poco dinero, no ingresar a plazos y tener una baja tasa de pagos a través de sus tarjetas, su límite de crédito es relativamente bajo. Socialmente, son personas de bajos ingresos que no tienen la posibilidad de acceder a compras constantes, prefieren ahorrar su dinero y no correr riesgos. A estos clientes se les denomina clientes inactivos.
| Clase | Característica | Nivel |
|---|---|---|
| Clientes Inactivos | Poder adquisitivo | Bajo |
| Capacidad de pago | Baja | |
| Consumo excesivo | Bajo |
La tercera clase está formada por los clientes con menor saldo en la tarjeta pero que realizan compras al contado, es decir, no ganan mucho dinero y su nómina en la tarjeta es baja, sin embargo, siguen consumiendo, realizan compras con frecuencia, ya sea de bienes o servicios, mediante tarjeta de crédito, generalmente a plazos o en cuotas porque no les es posible pagar al instante debido al poco dinero que tienen en sus cuentas. Además, el límite de pago es inferior a la media global de todos los clientes, debido a su bajo nivel de ingresos. No es el límite de crédito más bajo entre las clases porque, al realizar frecuentemente compras a plazos, su historial crediticio es bueno, sin embargo, el tiempo en el que pagan sus deudas no es favorable para su límite de crédito. Son personas de bajos ingresos a las que les apasiona satisfacer sus deseos frecuentes, aunque eso signifique pagar a plazos. Se les llama clientes activos.
| Clase | Característica | Nivel |
|---|---|---|
| Clientes Activos | Poder adquisitivo | Alto |
| Capacidad de pago | Bajo | |
| Consumo excesivo | Bajo |
En la cuarta clase se encuentran los clientes que utilizan más las tarjetas de crédito, ya que mantienen un alto índice de compras frecuentes al instante o a plazos, porque manejan una gran cantidad de dinero y mantienen un saldo para adquirir posteriormente cualquier bien o servicio. Por ello, tienen un alto perfil en la entidad bancaria y se benefician de la obtención de un mayor límite de crédito, además de retirar muy poco efectivo por adelantado. Socialmente, se les denomina personas de altos ingresos que gastan su dinero para satisfacer sus gustos, además de sus necesidades básicas. Estas personas son clientes potenciales.
| Clase | Característica | Nivel |
|---|---|---|
| Clientes Potenciales | Poder adquisitivo | Alto |
| Capacidad de pago | Alto | |
| Consumo excesivo | Alto |
Estrategias de mercado
Clientes pasivos, tienen compras muy bajas, debido a la falta de información sobre promociones y descuentos, para lo cual, desde la base de datos del usuario, se puede contactar un número telefónico y comenzar a hacer uso informativo de ese medio de comunicación. Asimismo, los asesores pueden estar en contacto mediante llamadas telefónicas, para difundir la información y asegurarse de que el usuario obtenga los beneficios. Para motivarlo, inicialmente se pueden generar promociones, acumulación de puntos que posteriormente pueden ser canjeados en algún bien o reembolsos en efectivo.
Clientes inactivos, se puede implementar un plan de incentivos, donde se proponga un orden de cuotas, que les permita ir a ciertos lugares para acceder a un producto como premio por el alto uso de las tarjetas de crédito, esta estrategia se puede llevar a cabo en las personas que más compran y con ello se promueve el uso constante.
Clientes activos, al mantener compras constantes, se puede implementar la acumulación de puntos, ya sea para obtener un producto gratis o con buenos descuentos y la exclusividad de participar en rifas de algún bien, como electrodomésticos. Asimismo, se pueden gestionar hasta 3 cuotas sin intereses, con el objetivo de que el cliente se motive y realice sus compras.
Para incentivar a los mejores clientes de tarjetas de crédito, se pueden generar recompensas o incentivos por el número de compras realizadas, ya sean mensuales o semestrales, asimismo, se pueden acumular millas para que los usuarios puedan obtener boletos sin altos costos en aviones y en la zona VIP, así como entradas a conciertos, zonas de entretenimiento, restaurantes, entre otros.
Nuevos clientes
Ver Código
ind.test <- Datos[8632:8636, 1:17] #5 clientes para realizar la prediccion
head(ind.test)
ind.test.coord <- predict(res.pca, newdata = ind.test)
ind.test.coord[, 1:3] # Miro los primeros dos componentes
# Utilizo el gráfico anterior y le anexo los nuevos individuos
p <- fviz_pca_ind(res.pca, repel = TRUE)
fviz_add(p, ind.test.coord, color ="blue")
nuevospuntos<-data.frame(ind.test.coord)
NP2<-data.frame(names = rownames(nuevospuntos), nuevospuntos)
Newgrafico<-data.frame((resultado_ACP$dudi)$li , Grupo)
X11()
#PC1 ; PC2
ggplot(Newgrafico, aes(x = Axis1, y = Axis2, color = Grupo)) +
geom_point() +
geom_point(NP2, mapping=aes(x=PC1,y=PC2, color = "Nuevos",
label = names), size=5.5)+ theme_bw()
Conseguimos clasificar a los clientes en clases en función de sus características en el uso de la tarjeta de crédito. Sin embargo, la institución bancaria no siempre tendrá el mismo número de clientes y estos no siempre presentarán el mismo comportamiento, por lo tanto, es necesario que el modelo creado tenga la capacidad de predecir a qué grupo debe pertenecer un cliente con nuevas características de gestión en cuanto al uso de su tarjeta de crédito.
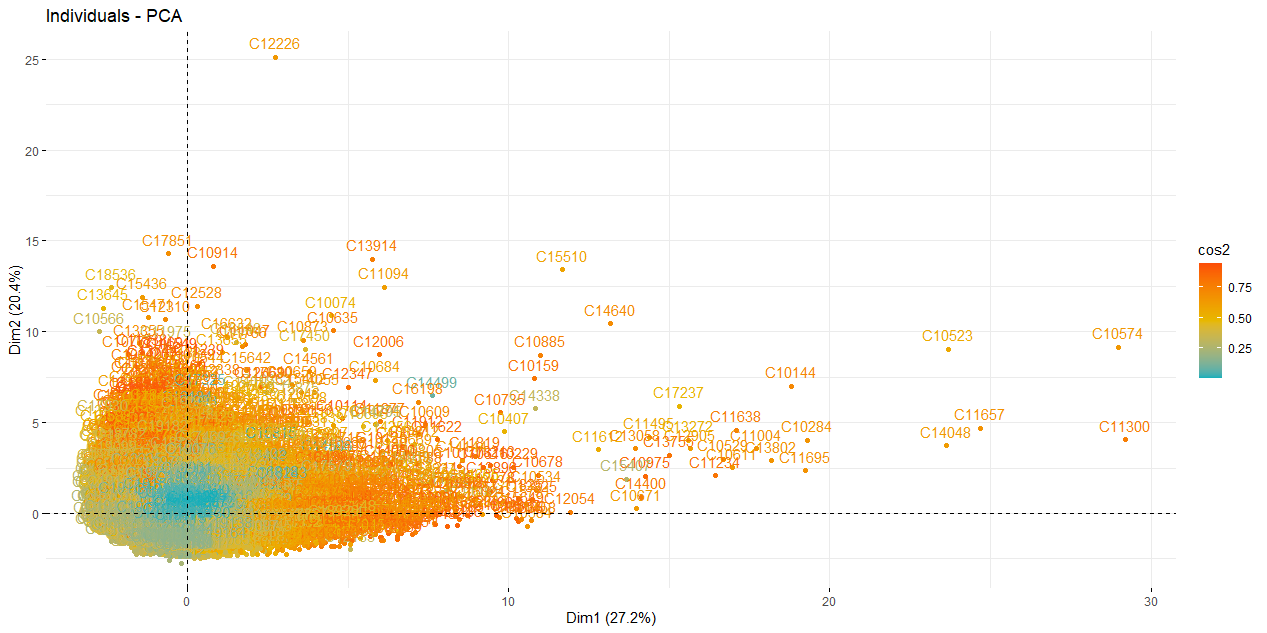
Dicho esto, se realizó una prueba de clasificación con 5 clientes sin grupo, para evaluar la eficacia del modelo en el momento de la catalogación. Esta prueba se realiza gráficamente, incorporando nuevos clientes representados por puntos morados en los planos previamente diseñados en el gráfico 4; Cabe mencionar que se conoce el valor de las variables características de los cinco clientes con respecto al uso de su tarjeta de crédito.
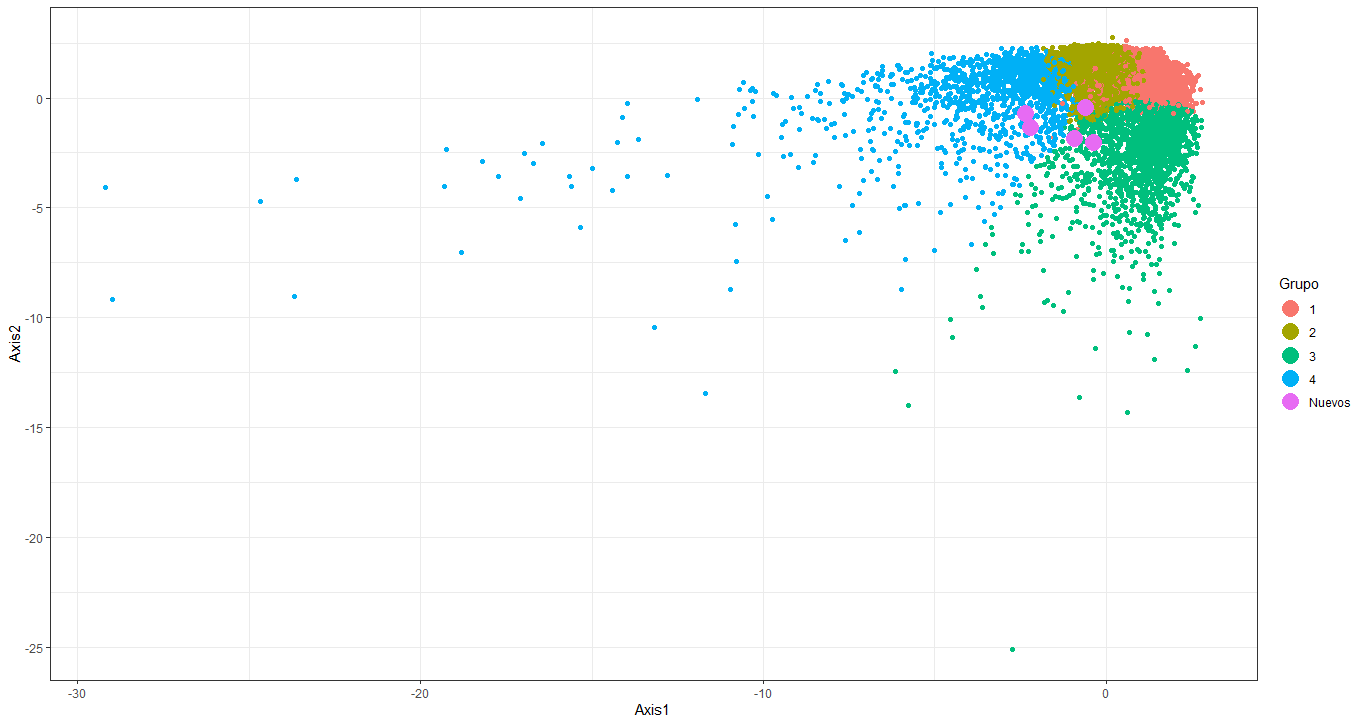
La visualización de los nuevos clientes en los grupos se ilustra mejor en el plano compuesto por los componentes 1 y 2, por lo que el análisis principal se realizó con este plano. Ahora bien, entre estos 5 clientes, el modelo clasificó a 3 de ellos como miembros del grupo 2 (clientes inactivos), y al resto como miembros del grupo 3 (clientes activos).
Aprendizaje supervisado
Realizamos un análisis supervisado utilizando la clasificación fundada en la agrupación. Utilizamos el 75% de los datos como entrenamiento y el 25% como prueba.
La clase que mejor se clasifica es la 4, Clientes potencial.
Ver Código
NuevaBase <- NuevaBase %>%
rename(grupo = Cluster ) %>%
mutate_at(c("grupo"), ~as.factor(.))
IndexEntrena<-createDataPartition(y = NuevaBase$grupo, p=0.75 , list = FALSE)
SP_entrena <- NuevaBase[IndexEntrena,]
SP_test <- NuevaBase[-IndexEntrena,]
SP_knnEntrenado <- train(grupo ~ .,
data = SP_entrena,
method = "knn",
tuneLength = 20)
class(SP_knnEntrenado)
SP_knnEntrenado
X11()
plot(SP_knnEntrenado)
SP_ctrl <- trainControl(method="cv", number = 5) #Metodo de validación cruzada
SP_knnEntrenado <- train(grupo ~ .,
data = SP_entrena,
method = "knn",
tuneLength = 20,
trControl = SP_ctrl,
preProcess = c("center", "scale"))
SP_knnEntrenado
x11()
plot(SP_knnEntrenado) # Aprece un nuevo k optimo! K=7
plot(SP_knnEntrenado,pch=8 ,bty="1",bg="seagreen2
nos", ylab = "Precision (Validación Cruzada)", xlab= "vecinos" ) #Grafica de K vs Precision
SP_knnPrediccion <- predict(SP_knnEntrenado, newdata = SP_test)
SP_knnPrediccion %>%
head(50)
prob_knnPrediccion <- predict(SP_knnEntrenado, newdata = SP_test, type= "prob")
prob_knnPrediccion %>%
head(10) #Probabilidades para catalogar a que grupo pertenece el cliente
confusionMatrix(SP_knnPrediccion, SP_test$grupo)
Ver Código
Confusion Matrix and Statistics
Reference
Prediction 1 2 3 4
1 463 118 4 1
2 182 1099 51 0
3 19 23 180 0
4 0 0 0 18
Overall Statistics
Accuracy : 0.8156
95% CI : (0.7986, 0.8317)
No Information Rate : 0.5746
P-Value [Acc > NIR] : < 2.2e-16
Kappa : 0.665
Statistics by Class:
Class: 1 Class: 2 Class: 3 Class: 4
Sensitivity 0.6973 0.8863 0.76596 0.947368
Specificity 0.9177 0.7462 0.97816 1.000000
Pos Pred Value 0.7901 0.8251 0.81081 1.000000
Neg Pred Value 0.8721 0.8293 0.97159 0.999533
Prevalence 0.3077 0.5746 0.10890 0.008804
Detection Rate 0.2146 0.5093 0.08341 0.008341
Detection Prevalence 0.2715 0.6172 0.10287 0.008341
Balanced Accuracy 0.8075 0.8162 0.87206 0.973684

